Money Management pamati. I.

Īstenībā ir svarīgi pareizi interepretēt
signālus, ko ģenerē indikātori
https://www.bcs.ru/forum/ 

Dmitrijs Tolstonogovs
TS Research Group
http://www.tsresearchgroup.com

Cilvēki vienmēr ir gribējuši zināt noslēpumu, kā vinnēt biržā. Tajā pašā laikā jaunas naudas pievilināšanas tirgum industrija, ar grāmatu ar attiecīgiem nosaukumiem, metastokiem un visdažādākajiem finamiem, ekspluatējot mūsu uzskatus, liek mums meklēt nepareizas lietas nepareizās vietās. Mes meklējam burvju indikātoru vai treidinga sistēmu, kas ļautu mums vinnēt 90 % gadījumu.

Es atradu tādu sistēmu. Daudzajos testos tā gandrīz nekad neuzrādīja mazāk kā 90 % vinnestu. Viena tāda testa rezultāti Omega Research TradeStation formātā ir doti tabulā 1.

Total Net Profit	$562.70		Open position P/L	($75.60)
Gross Profit	$1,269.40		Gross Loss	($706.70)
Total # of trades	276		Percent profitable	92.75%
Number winning trades	256		Number losing trades	20
Largest winning trade	$54.90		Largest losing trade	($126.50)
Average winning trade	$4.96		Average losing trade	($35.33)
Ratio avg win/avg loss	.14		Avg trade (win & loss)	$2.04
Max consec. Winners	39		Max consec. losers	2
Avg # bars in winners	1		Avg # bars in losers	17
Max intraday drawdown	($177.30)
Profit Factor	1.80		Max # contracts held	1
Account size required	$177.30		Return on account	317.37%

Tab.1 Viena no testiem rezultāti uz dienu vēsturiskajiem datiem РАО EЭС, Krievijā. (neietverot komisijas un noslīdējumus (slippage)).

Atklāts šīs sistēmas kods ir parādīts pielikumā 1: var pārrakstīt to Omega TradeStation vai SuperCharts[1] - un vinnēt, tādā nozīmē, kā tas parasti tiek saprasts: iegūt peļņu gandrīz katrā no darījumiem. Galvenais sistēmas noslēpums ir pseido gadījuma skaitļu ģenerātors (TradeStation tas ir pārāk “pseido”-gadījuma, bet tas nav principiāli. Tālāk viss kā parasti: ja pozīcija ir ar peļnu – aiztaisam to. Ja tirgus iet pret mums – kļūstam par investoriem. Man bija prieks vērot un sadarboties ar divu brokeru kompāniju klientiem divus gadus, - varu droši apgalvot, ka lielākā daļa spēlētāju pieturas tieši šai stratēģijai, izņemot to, ka gadījuma skaitļu ģenerātors formāli tiek aizvietots ar analītiķu prognozēm, tehniskās analīzes indikātoru signāliem, dīlinga zāles kamiņu viedokli vai neizskaidrojamiem, pēkšņiem impulsiem.

{**************************************************************************************

                                    Random System №1.

                                    Copyright (c) 2001   DT

***************************************************************************************}

Inputs:            Bias(.025),        {Random entry parameter}
                        mmstp(100),      {Stop-loss parameter}
                        pflim(.1),            {Profit target limit}
                        maxhold(50);     {maximum holding period};

Var: Trigger(0), Signal(0), ATR(0), num(1);

trigger = random(1);
if trigger < bias then signal = -1;
if trigger > 1 - bias then signal = 1;
ATR = XAverage(TrueRange,50); 

{Random Entry}

If signal = 1 then Buy("Random_Mkt.LE") num contracts next bar at open;
If signal = -1 then Sell("Random_Mkt.SE") num contracts next bar at open;

{Standartized Exits}

if marketposition > 0 then begin

            ExitLong ("MM.LX") Next Bar at EntryPrice - mmstp*ATR stop;
            ExitLong ("Pt.LX") Next Bar at EntryPrice + pflim*ATR limit;
            if barssinceentry >= maxhold then
            ExitLong ("Hold.LX") at close;
end;

if marketposition < 0 then begin

            ExitShort ("MM.SX") Next Bar at EntryPrice + mmstp*ATR stop;
            ExitShort ("Pt.SX") Next Bar at EntryPrice - pflim*ATR limit;
            if barssinceentry >= maxhold then
            ExitShort ("Hold.SX") at close;

end;

Problēma ir apstāklī, ka vinnēt biržā, un pelnīt tajā naudu – nepavisam nav viens un tas pats. Peļņas pamatā, kas iegūta piemērā Nr. 1., ir liela daļa veiksmes, - veiksmīga rinda gadījumu skaitļu – lielākajā daļā testu šī stratēģija nez zaudējumus.

Tomēr ja izmainīsim ieejas parametrus uz saprātīgākiem, pftlim vienādu ar 4, mmstp vienādu ar 1, bet maxhold vienādu ar 10, tad šī sistēma lielākājā daļā testu būs peļņu nesoša.

 Galvenā spekulāciju principa realizācija – ātri aiztaisīt zaudējumus nesošās pozīcijas un ļaut peļņai augt – plus money management, kas ir spekulāciju pamatā, ļauj pelnīt pat izmantojot gadījuma skaitļu ģenerātoru. Lielākā daļa cilvēku darbojas tieši pretēji šim likumam: viņi ļauj zaudējumiem augt, cerot, ka tirgus pagriezīsies, un pierādīs galu galā, ka viņiem bija taisnība, un – ātri aiztaisa peļnu nesošās pozīcijas, lai nofiksētu savu taisnību. Pratiski visi iesācēji, un daudzi, kas uzskata sevi par profesionāļiem, kā parāda mūsu pieredze, ir pārliecināti, ka māka prognozēt tirgu ir asociējama  ar māku  pelnīt tirgū. Vinnests katrā dotajā darījumā viņiem nozīmē savu prognozes spēju apstiprinājumu, un sekojoši, mākas nopelnīt, apstiprinājumu.

 Cilvēkam, kas nav pazīstams ar treidingu kā biznesu, fakts, ka “veiksmīgai investēšanaiun treidingam nav nekāda sakara ar prognozēšanu”[1], var likties kā pretruna veselajam saprātam. Treideru aprindās pazīstamais Oļegs Guščins saka: Ir divas ziņas – slikta un laba. Sliktā ziņa – tirgu prognozēt nav iespējams. Labā ziņa: Lai pelnītu tirgū, prognozēt nevajag. Pie tam runa te iet par lieliem vinnestiem tajos gadījumos, kad jums ir taisnība, bet ne par vinnestiem katrā darījumā. Pie tam zaudējumu skaits var pārsniegt vinnestu skaitu, t.i. pilnīgi pieņemami ir prognozēt sliktāk, nekā mēs to darītu mētājot monētu. Pēc izcilā treidera Paul Tudor Jones, vārdiem, “Es varu tikt apstādināts četras vai piecas reizes treida laikā, pirms tas tiešām sāks kustību”.[2] Citiem vārdiem, Paul Tudor Jones var vinnēt tikai kaunpilnos 20 – 25 % gadījumu.

Tomēr viņa rēķinā ir pieci gadi ar gada ienākumu trīszīmju procenta veidā pie ļoti zemām pamatkapitāla korekcijām.Gandrīz 100 % no ļoti ievērojamiem vinnestiem Stīvam Kohenam (Steve Cohen) ir 5 % no darījumiem, pie tam tikai 55% darījumu ir vinnesti. Neskatoties uz to, pēdējo 7 gadu laikā viņa vidējais ienākums sastāda 90 % gadā, un viņam ir bijuši tikai trīs mēneši ar zaudējumiem, pie tam sliktākais no tiem bija -2%.

Profesionāļu plaši pielietotās metodes trenda sekošanai, kā likums, nes no 30 – 40% vinnestu. Pie tam vinnesta vai zaudējuma lielumam katrā konkrētā darījumā nav nozīmes. Svarīgi ir tikai tas, ka naudas daudzums kas tiek nopelnīts vidēji par katru darījumu ir pozitīvs. Šis lielums tiek saukts par matemātisko cerību.  Matemātiskā cerība ir vinnestu varbūtību summa reizināta ar vinnestu lielumu, mīnus zaudējumu varbūtība, kas reizināta ar zaudējumu lielumu:

 Ε = S_i(Vinnesta varbūtība * vinnests_i ) - S_j(Zaudējuma varbūtība_j * zaudējums_j )

 Vienkāršotā veidā matemātisko cerību var definēt kā vinnesta varbūtību, kas reizināta are vidējo vinnnestu, mīnus zaudējuma varbūtība, kas reizināta ar vidējo zaudējumu. Statistiskās atskaites terminos Omega Research TradeStation tas ir:

 Е = Percent profitable * Average winning trade – (1 - Percent profitable) * Average losing trade.

Kļūdaini asociējot vinnesta iespējamību ar matemātisko cerību, spēlētāji meklē spēles metodes ar lielu vinnesta iespējamību. Tomēr tādām metodēm bieži vien ir negatīvs matemātisko cerība. Tas nozīmē, ka agri vai vēlu, spēlējot šīs spēles viņi zaudēs visu naudu.

 Vienā no diskusijām PTC[3] forumā analītiķiem, viens no Eliota teorijas[4] piekritējiem paziņoja: “Tirgus nav kazino, mēs neliekam likmes”. Atšķirībā ne Eliotiķiem, kam dzīve rit pa iepriekš zināmu sarakstu, mēs lieka likmes tirgū. Tā kā darījuma rezultāts nav zināms, katrs darījums ir likme, kurā mēs vinnējam vai zaudējam zināmu summu naudas. Galvenās atšķirības starp likmēm kazino (azartspēlēs) un likmēm tirgū (spekulācijās), atskaitot meitenes un bezmaksas dzērienus, ir pirmkārt, azartspēles rada risku, bet spekulācijas tirgū objektīvi pārdala eksistējošo risku, un otrkārt, tirgū treideris var radīt sev statistiskas priekšrocības, t.i. pozitīvu matemātisko cerību.

 Apskatīsim likmi uz krāsas izkrišanu ruletes spēlē kazino. Ir 18 sarkanie sektori, un ir 18 melnie sektori un zero (amerikāniskajā variantā liekas ir arī dubultzero). Matemātisko cerība vinnestam vienreizējai likmei sastāda 18/37 – (18 + 1)/37 = -1/37. Vidēji kazino vinnē vienā spēlē uz vienu spelētāju šo lielumu, kas reizināts ar likmes lielumu.  Neskatoties uz dažiem lieliem klientu vinnestiem, kopumā kazino paliek vinnestā – pateicoties matemātiskajam gaidāmajam  savā labā, ko sauc arī par “kazino priekšrocību”, un ne tāpēc, ka krupjē māk prognozēt, kur apstāsies bumbiņa.

Taisnības labad jāatzīmē, ka ir zināmi “spēlētāja priekšrocības” gadījumi kazino: Matemātiķis Edward Thorp izstrādāja stratēģijas ar pozitīvu matemātisko cerību, blackjack spēlē, (acīte), ko veiksmīgi pielietoja Lasvegasas kazino. Kad viņu pārstāja laist pāri kazino slieksnim, viņš publicēja savas metodes,[5] pēc kā acītes noteikumos tika ieviestas izmaiņas, kas laupīja šīm stratēģijām “spēlētāja priekšrocības”. Toreiz, 60-to gadu beigās, Thorp ieinteresējās par akciju tirgu un sāka vadīt privātu investīciju kopu: “Nopietns konkurents tajā laikā bija nākamais nobeļa prēmijas laureāts Harry Markowitz. Pēc 20 mēnešiem mūsu rezultāts parādija vinnestu +39.9 % pret + 4.2 Dow-Jones indeksa. Markowitz pēc pāris gadiem nolaidās uz “mīnusu”, bet mēs esam apmierināti ar mūsu saglabātajiem rezultātiem, aptuveni 20 % ikgadēji ar standarta novirzi aptuveni 6% un tās nulles korelāciju ar tirgu”.[6]

Tirgus dod iespēju spēlēt spēles ar pozitīvu matemātisko cerību. Tas ir nepieciešamais noteikums veiksmīgai spēlei biržā. Pie tam, kā uzskata Ralfs Vinss, “nav svarīgi, cik negatīvam vai cik pozitīva ir matemātiskā cerība, galvenais, vai tā ir pozitīva vai negatīva”. [7] Apgalvojums, pēc mūsu domām, apstrīdams: Lielāka matemātiskā cerība labāka par mazāku. Bez matemātiskās cerības, lielākajai daļai ir problēmas ar riska saprašanu. Piemēram, vienas reģionālās investīciju kompānijas, kuras aktīvi 1997. gada vasarā pārsniedza miljonu dolāru, direktors, vēsturnieks pēc izglītības, bija pārliecināts, ka “risks neeksistē un tāpēc to nevar nomērīt” un ka, “nedrīkst tirgot akcijas ar zaudējumiem”. Tad ko runāt par neprofesionāļiem. Risks eksistē, un to var noteikt un nomērīt ar daudz un dažādiem līdzekļiem. Ekonomisti uzskata, ka risks – tas ir mainīgums (volatility), kas tiek mērīts kā standarta aktīva izmaiņu novirze. [8] Šis definējums gan der tikai “pērc un turi” stratēģijām.  Daudz adekvātāk priekš spekulanta ir riska definēšana, kā standarta kapitāla izmaiņu novirze.[9] Neiedziļinoties sīkumos, atzīmēsim, ka risks, saskaņā ar šo definīciju, lielā mēra tiek nenovērtēts. Saskaņā ar Mērfija likumiem (nejaukt ar CNBC tehnisko analītiķi), sliktākais vēl tikai priekšā. Mēs izmantosim sekojošu definīciju: risks, tas ir naudas daudzums, ko jūs esat gatavi zaudēt, pirms iziet no zaudējumu nesoša darījuma.

Pirms pozīcijas atvēršanas ir nepieciešams noteikt punktu, kurā mēs aiztaisīsim zaudējumus nesošu pozīciju, ar mērķi saglabāt kapitālu, t.i. tā saucamo stop-loss[10], vai arī attaisīsim pretēju pozīciju, kad būsim pārliecināti, ka tirgus virzās pret mums (stop-and-reverse). Starpība starp ieejas punktu, un izejas punktu pēc stopa, kas reizināta ar lotu daudzumu, ir sākotnējais risks, jeb 1 R[11], neatkarīgi ne no tā kādu metodi izmantojam, vai kādās mērvienībās mēs nosakam stopa līmeni: latos, procentos vai papagaiļos. Jāpasvītro, ka mūsu riska apzīmējums nav viens un tas pats kas 1 R. Risks – tas ir cik mēs zaudēsim reāli. Risks var nopietni pārsniegt 1 R, stopa neizpildes gadījumā disciplīnas neievērošanas gadījumā,[12] gapu (gaps) pret pozīciju esamības dēļ, vai noslīdējumu (slippage), lielāku nekā gaidīts dēļ. Arī peļnu mēs varam mērīt riska vienībās uz akciju, vai R-os. Terminos, kas attiecināmi uz R, galvenais spekulācijas princips var tikt definēts tā: saglabāt zaudējumus uz 1 R līmeņa, cik tas ir iespējams, un ļaut peļņai jo lielākus kārtējos R. Matemātiskā cerība uz pakāpeniski pieaugošajiem R nozīmēs to, cik mēs vidēji vinnējam vai zaudējam vienā darījumā uz vienu riska vienību. Lai atrastu matemātisko cerību attiecīgajiem R, mums jāievada savu darījumu rezultāti tabulā ar sekojošām kolonām:

Lotu skaits

Peļņa vai zaudējumi

Sākotnējais risks

Kārtējais  R

Peļņai vai zaudējumiem jāņem vērā gan komisijas brokerim gan arī noslīdējumus. R tiek atrasts dalot otro kolonu ar trešo. Tagad, lai atrastu matemātisko cerību, ir jāsummē ceturtā stabiņa rezultāti un jāizdala ar darījumu skaitu. Dotā metode der arī intuitīvajam treidingam.

Apskatīsim piemēru. Tirgosim PAO ЕЭС un ММВБ akcijas. (no 05.29.1997), pēc sekojošiem noteikumiem (tie ir paši vienkāršākie, ko varējām iedomāties).

Pērkam vienu lotu, ka vidējā dienas cena ((high + low)/2) kļūst lielāka par savu minimālo vērtību par 4 kapeikām;

 Pārdodam vienu lotu, ja vidējā dienas cena ((high + low)/2) kļūst mazāka par savu maksimālo vērtību par 4 kapeikām;

Atskaitam no katra darījuma 1 rubli par komisijām un noslīdējumiem.

***************************************************************************

                                   The Simplest System №2.

                                    Copyright (c) 2001   DT***************************************************************************}

Input:   Price((H+L)*.5), PtUp(4.), PtDn(4.);
Vars: TrendLine(C), LL(99999), HH(0), num(1);
if MarketPosition <= 0 then begin
if Price < LL then LL = Price;
if Price cross above LL + PtUp*.001 then begin

                        buy("Simpl.LE") num contracts next bar at market
                        HH = Price;

end;
end;

if MarketPosition >= 0 then begin

            if Price > HH then HH = Price;
            if Price cross below HH - PtDn*.001 then begin

                        Sell("Simpl.SE") num contracts next bar at market
                        LL = Price;

end;
end;

Pielikums 2. Vienkāršākā sistēma №2

{**************************************************************************************

Expectancy Output                                

Copyright (c) 2001   DT

***************************************************************************************}

Var: RMult(1),R1(1), Trades(0);
Trades = TotalTrades;
R1 = PctUp*.001*BigPointValue;
RMult = PositionProfit(1)/R1;
If barnumber = 1 then
print(file("D:TS_ExportM-trading.csv"),"Qty",",","Profit",",","Initial Risk",",","R multiple");
If Trades <> Trades[1] then
print(file("D:TS_ExportM-trading.csv"),Num:10:0,",",PositionProfit(1):10:4,",",R1:10:4,",",RMult:10:4);         

Pielikums 3. Datu ievade failā, matemātiskās cerības noteikšanai.

Pielikumā 3 dots kods, ko nepieciešams pievienot kodam, kas dots pielikumā 2, lai izvestu nepieciešamos datus norādītajā failā D:TS_ExportM-trading.csv (protams, jānorāda savs fails).

Tādā veidā iegūto failu var analizēt ar Excel palīdzību (Excel-Services-Data analysis). Kārtējo R histogramma (zīm.1) lieliski attēlo tendencies sekošanas filozofiju. Viegli ieraudzīt, ka lielākā daļa darījumu nes zaudējumus no viena līdz diviem R (mediāna –1.35, peļņu nesošo darījumu skaits – 37 %), ir divi darījumi ar zaudējumiem, kas pārsniedz 10 R, un piecpadsmit darījumi, kuros peļņa pārsniedz 10 R. Histogramma ir izkropļota uz labo pusi (asimetriskums 3.46). Pie tam peļņa no viena darījuma sastāda 53.15 R! Matemātiskā cerība šajā piemērā sastāda 0.24 R t.i. uz katru riska rubli mēs vidēji ceram uz peļņu 1.24 Rbl.

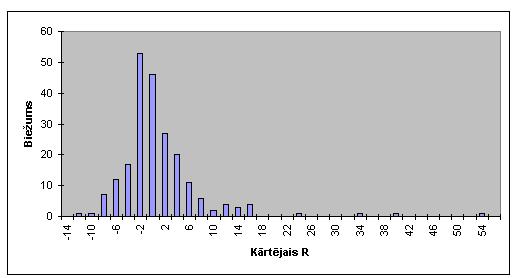
Zīm. 1. Kārtējo R izkliede

Un tā – mums ir vinnējoša stratēģīja – ko vēl vairāk? Atlicis tik atvērt kontu pie brokera, - pie mums, piemēram, - un laist uz visu naudu pēc pilnas programmas.

Šeit sākas pats galvenais, sekojoši – money management. Skaidrībai pievedīsim pāris faktus.

Ralfs Vinss izdomāja spēli, kurā vienīgais parametrs bija likmes lielums. Spēlei viņš savāca 40 zinātņu kandidātus, t.i. kā minimums cilvēkus ne pašus muļķīgākos. Vienīgais noteikums bija, ka neviens no viņiem nedrīkstēja būt profesionālis, un neviens nebija studējis statistiku. Zinātņu kandidāti spēlēja spēli, kurā tika ģenerēti 100 gadījuma rakstura darījumi, viens darījums katru reizi. Visi sāka ar USD 1000, un pirms katra darījuma veikšanas bija jāpieņem viens vienīgs lēmums: kādu summu – no USD 0 līdz visam kapitālam – likt. 60 % gadījumu viņi vinnēja summu ko lika, bet 40 % gadījumu zaudēja summu, ko bija likuši. Šai spēlei matemātiskā cerība ir 20 centi uz katru riska dolāru, t.i katrs dolārs, ar ko nākotnē riskējam, dod atpakaļ dolāru, un divdesmit centus pa virsu. Zinātņu kandidāti veica 100 darījumu, kas ir pietiekami matemātiskās cerības realizācijai. Beidzot spēli, visi to pabeidza ar dažādiem rezultātiem. Uzminiet, cik no viņiem palielināja savu sākotnējo kapitālu? Divi no četrdesmit. 95 % zinātņu kandidātu zaudēja naudu spēlē ar pozitīvu matemātisko cerību![1].

Van Tharp dod vēl iespaidīgāku piemēru[2]. Dow Jones Telerate TAG (Technical Analysis Group) āzijas tūres laikā viņš uzstājās ar lekciju 8 pilsētās 50 – 100 klausītāju priekšā. Lielākā daļa no tiem bija profesionāli treideri, kas darbojās lielās kompānijās vai bankās, un tirgojās ar akcijām, obligācijām vai valūtas kursiem FOREX. Dažu tēmu ilustrācijai viņs piedāvāja klausītājiem uzspēlēt spēli, analoģisku Vinsa spēlei. Tur, kur izkrita lielākā daļa zaudējumu, vairak nekā puse auditorijas – profesionālu treideru – zaudēja naudu.

Un vel viens piemērs no analītiķu dzīves. Treideris Oļegs Najdenovs, kas tagad ir pārvācies uz Ameriku, deva spēlēt līdzīgu spēli savai paziņai, kas strādā par vadošo analītiķi Charles Schwab. [3] Pirmajā spēles līmenī tiek dots R ar matemātisko cerību 0.45 un 60 % vinnestiem. Lai pārietu uz nākošo līmeni, 100 spēļu laikā jāpalielina kapitāls par 50 %.

Rezultāts ir sekojošs: “Viņa jau otro dienu nevar iziet uz nākošo līmeni”.

Brinson, Singer un Beebower [4] 1991 gadā publicēja pētījumu, par 82 aktīvu portfeļū rezultativitāti 10 gadu laikā, kas parādīja, ka 91.5 % no peļņas bija aktīvu izvietošanas rezultāts. Aktīvu izvietošana šajā pētījumā nozīmē, kāda kapitāla daļa bija izvietota akcijās, obligācijās vai naudā. Tikai 8.5 % rezultātu tika skaidroti ar to, kādas tieši akcijas vai obligācijas tika pirktas un kad.

Uzspēlēsim to pašu spēli, ko zinātņu kandidāti pie Vinsa. Ja nebūtu bijis riska, tad katra darījuma rezultāts būtu bijis zināms, un tad būtu loģiski katru reizi likt visu esošo kapitālu uz spēles. Tad katrs zinātņu kandidāts saņemtu $1000*(1.2^100) = $82,817,974,522.01. Reāli, ja mēs pirmajā spēlē liekam likmi USD 1000, tad mums ir 40% iespēja pazaudēt visu jau pirmajā reizē. Pat, ja mums noveicas, un mums būs USD 2000, tad visa kapitāla likšana uz spēles nākošajā reizē būs tik pat muļķīga, kā pirmajā reizē. Pieņemsim, mēs katru reizi liekam pa USD 200. Šajā gadījumā, ja pirmās piecas reizes būs zaudējumi, mēs atkal zaudēsim visu kapitālu. Protams, šāda iespējamība ir pavisam neliela – nedaudz vairāk kā 1 %. Bet vai mēs esam gatavi 1% riskam zaudēt visu pie pirmajiem pieciem neveiksmīgajiem darījumiem? Pieņemsim, mēs zaudējām pirmajos divos darījumos, tas var notikt ar varbūtību 16%. Mēs zaudētu 40 % no kapitāla, un mums vajadzētu palielināt konta lielumu par 67 % lai tikai atgūtu sākotnējo kapitālu. Šo efektu sauc par asimetrisko leverāžu. [5] No tab. Nr. 2 redzams,  ka zaudējumi, kas lielāki par 50 %, pieprasa milzīgu, maz iespējamu peļņu, lai tikai atjaunotu sākotnējo kapitāla lielumu. Rezultātā, ja mēs riskējam ar lielu summu no mūsu konta un zaudējam, iespējas palikt beigu beigās ar peļņu ir ļoti mazas.

 Kandidātu zaudējums var tikt izskaidrots, ne tikai ar pārāk lielām likmēm. Plaši sastopams malds, ko sauc par spēlmaņa kļūdu: mēs tiecamies ticēt, ka pēc zaudējumu sērijas vinnesta iespējamība pieaug, un palielinām likmes. Tomēr vinnesta iespējamība dotajā spēlē neatkarājas no iepriekšējiem darījumiem un pa vecam paliek 60%.

Pieņemsim, ka katru reizi liksim noteiktu daļu no kapitāla daudzuma procentos, un pēc katra gadījuma pierakstīsim tekošo kapitālu. Darīsim to atkal un atkal pa 100 reizēm. Pēc pietiekami liela sēriju skaita (piemēram 1000), mēs varēsim novērtēt tirdzniecības rezultātu sadalījumu. Acīmredzami, ka neskatoties uz vienādajiem spēles noteikumiem, lielākajā daļā no sērijām saņemsim dažādus peļņas rādītājus – zaudējumu un vinnestu gadījuma rakstura dēļ. Šo metodi sauc par Monte – Karlo modelēšanu.

Spēles rezultātu analīzei, bet mēs 1000 spēļu sēriju laikā ieguvām 1000 izdevīguma variantus, izliksim visus variantus virknē no mazākā līdz lielākajam. Pēc sadalīsim tos pa 100 daļās kas ir vienādas pēc skaita variantos – katrā simtajā to daļā (to sauc arī par percentīli), būs tādējādi, pa 10 rezultātu variantiem.  Pirmajā percentīlī būs savākti 10 sliktākie varianti, bet šī percentīļa robeža (10e vērtība) attieksies uz to, kas parasti tiek formulēts šādi: “1 % gadījumu rezultāti būs sliktāki par ... vērtību”. Statistikā šādu percentīli ir pieņemts apzīmēt ar ar k-1. 50 percentīļa robeža (k-50) būs attiecināma uz frāzi “50 % gadījumu rezultāti būs sliktāki par....vērtību”.

Tabulā 3 ir parādīti rezultāti 1000 spēles variantiem pie dažādām likmēm, procentos no kapitāla.

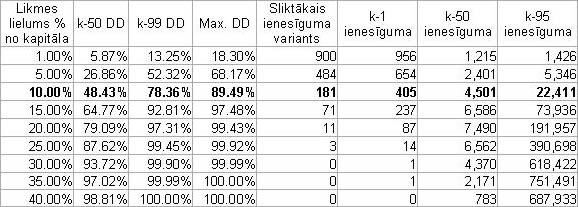
Tab. 3. “Spēles zinātņu kandidātiem” modelēšana pēc Monte-Karlo metodes

Pie likmes 10 % no kapitāla katrā darījumā (rinda ir atzīmēta tabulā), pie sākuma kapitāla USD 1000, minimālais kapitāla lielums pēc 100 darījumiem 1000 spēlēs sastādīja USD 181. 1 % no visiem mēģinājumiem mūsu kapitāls bija mazāks par USD 405 (k-1 ienesīguma). 50 % gadījumu gala rezultāts bija USD 4501 un mazāk (k-50 ienesīguma). 95 % gadījumu gala kapitāls bija mazāks, kā USD 22441 (K-95 ienesīguma, un, attiecīgi 5% gadījumu, kapitāls izrādījās lielāks, nekā USD 22411.

Apskatīsim drawdowns (DD tab. 3). Drawdown – tā ir starpība starp kapitāla maksimālo vērtību un tā nākošo minimumu līdz tam, kad kapitāls sasniegs jaunu maksimumu. Pie likmes 10 % no kapitāla 50% gadījumu DD bija 48%, 1% gadījumu – lielāks par 78%, un maksimālā vērtība sastādīja gandrīz 90 % kapitāla. Pie likmēm, kas bija augstākas par 30 % no kapitāla lieluma, mēs praktiski esam nolemti izputēšanai. Vēl reiz atgādināsim, ka spēlei ir pozitīva matemātiskā cerība – pie zaudējumu un vinnestu attaicības 40 % pret 60 %, vinnesta lielums attiecas pret zaudējuma lielumu kā 1 pret 1.

Steve Cohen apgalvo, ka “kopējā kļūda, ko pielaiž treideri...ir tas, ka viņi ņem pārāk lielas pozīcijas attiecībā pret saviem portfeļiem. Pēc tam, kad akcija sāk virzību pret viņiem, sāpes kļūst pārāk stipras, lai vadītu tās, un viņi galu galā paniko, vai iekrīt stingumā”. [1]. Apskatāmie piemēri parāda likmes lieluma svarīgumu spēlēs ar nenoteiktu iznākumu.

Kas tad ir money management? Mēģinot meklēt internetā, pēc šiem atslēgvārdiem, mēs ieguvām personālo finanšu pakalpojumus, ieteikumus, kā vadīt svešas finanses, Turtle Trading u.t.t. Saskaņā ar Van Tharpu:

Money management – nav nekas no zemāk uzskaitītā: 

-          tā nav sistēmas daļa, kas diktē, cik jūs zaudēsiet dotajā darījumā;
-          tā nav instrukcija, kad iziet no peļņu nesoša darījuma;
-          tā nav diversifikācija;
-          tā nav riska kontrole;
-          tā nav bēgšana no riska;
-          tā nav sistēmas daļa, kas maksimizē produktivitāti;
-          tā nav sistēmas daļa, kas saka, kur investēt.

Money management – tā daļa no tirdzniecības sistēmas, kas saka “cik”. Cik investīciju nominālus jātur dotajā momentā? Cik riska jāuzņemas?[2]

Citiem vārdiem, money managemt – tā likmes lieluma vadība. Visradikālāko apzīmējumu dod Ryan Jones [3]: money management ierobežojas  tikai ar to, ar kādu summu no jūsu konta riskēt nākošajā darījumā.

Pievērsiet uzmanību, ka šī definīcija neasociē money management ar jau atvērtas pozīcijas vadību, kaut gan Van Tharp to pieļauj.

1. Jack Schwager. Stock Market Wizards. HarperBusiness, 2001. lpp. 311.
2. Jack D. Schwager. Market Wizards. HarperBusiness, 1993.
3. http://www.forum.rtsnet.ru
4. Teorija, kas sludina kādas augstākās kārtības esamību biržu cenu izmaiņās. Mēs nekritizējam pašu teoriju, kas satur daudzas racionālas idejas, bet gan tās dogmatisko traktējumu.
5. Edward Thorp. Beat the Dealer. Random House, 1962.
6. Edward Thorp. The Kelly Criterion in BlackJack, Sports Betting, and the Stock Market./The 10^th International Conference on Gambling and Risk Taking. 1997.
7. Ральф Винс. Математика управления капиталом. Изд-во Альпина, М. 2000
8. У. Шарп. Инвестиции.
9. Perry Kaufman. Smarter Trading. McGrow-Hill, 1995.
10. Современный трейдинг №2 2001, с.22-27.
11. Van K. Tharp. Trade Your Way To Financial Freedom. McGraw-Hill, 1998, с.74.
12. Mūsu ober-leitnants Makovecs vienmēr ir teicis: “Disciplīna, stulbeņi, ir nepieciešama. Nebūtu disciplīnas, jūs vēl kā mērkaķi pa kokiem ložņātu.”. Jaroslavs Hašeks. Brašā kareivja Šveika piedzīvojumi.