EdSeykota
Risks
Risks – tā ir iespēja pazaudēt. Ja mums pieder dažas akcijas un pastāv iespēja, ka cenas kritīsies, tas nozīmē, ka mums draud briesmas. Akcija nav risks un zaudējums arī nav risks. Iespēja zaudēt – tas ir risks. Tikmēr, kamēr mums pieder akcijas, mums draud briesmas. Vienīgā iespēja vadīt risku ir akciju pirkšana un pārdošana. Akciju pārvaldīšanas jautājumā un tieksmē pēc peļņas risks ir neizbēgams un labākais, ko mēs varam darīt, ir – pārvaldīt risku.
Risku pārvaldīšana
Pārvaldniekam ir jānorāda un jākontrolē. Lai risku pārvaldītu ir nepieciešama norādīšana un kontrole pār iespējamajiem zaudējumiem. Risku menedžera darbs ir risku izmērīt, bet pēc tam akcijas vai nu pārdodot, vai pērkot, šo risku palielināt vai samazināt.
Piemērs ar monētas mešanu
Teiksim, mums ir monēta mešanai, kura ar vienādu ticamību var nokrist vai nu ar ciparu, vai ģerboni uz augšu. Piemērs ar monētas mešanu palīdzēs iztēloties risku pārvaldīšanas koncepciju.
Notikuma VARBŪTĪBA – tā ir varbūtība, kas tiek izteikta skaitļu attiecībā starp faktiski notikušo un to, kas varēja notikt. Piemēra, ja monēta no 100 reizēm 50 nokrīt ar ģerboni uz augšu, tad ģerboņa iespējamība ir 50 %. Ievērojiet, ka varbūtībai ir jāatrodas starp nulli (0.0 = 0 % ≈ neiespējamība) un vieninieku (1.0 = 100 % = neizbēgamība).
Lūk, spēles noteikumi: (1) mēs sākam ar 1,000 $, (2) mēs vienmēr izdarām likmi uz to, ka izkritīs ģerbonis, (3) likmē mēs varam ieguldīt jebkuru naudas summu, kura ir mūsu rīcībā, (4) ja izkritīs cipars, tad mēs zaudējam likmi, (5) ja izkritīs ērglis, tad mēs savu likmi nezaudējam, bet iegūstam divreiz tik daudz, cik liela bija likme, un (6) monēta ir taisnīga, tāpēc ģerboņa iespējamība ir 50 %. Šī spēle ir tāda pati, kā dažas treidinga metodes
Šajā gadījumā mūsu VEIKSME ir vienlīdzīga laimesta iespējamībai, vai 50 %. Mēs vinnēsim 50 % gadījumu. Mūsu atalgojums ir 2 : 1, jo mēs vinnējam 2 uz katru likto 1. Mūsu RISKS ir naudas daudzums, kuru mēs ieguldām likmē un nākamajā metienā pakļaujam riskam. Šajā gadījumā mūsu veiksme un atalgojums paliek nemainīgas. Mainīties var tikai likme.
Citās sarežģītākās spēlēs, piemēram, tirdzniecībā ar reālām akcijām, veiksme un atalgojums var mainīties vienlaikus ar tirgus stāvokļa izmaiņām. Šķiet, ka treideri tērē ļoti daudz laika un spēkus mēģinot izmainīt veiksmi un atalgojumu, bet tas ir veltīgi, jo šie parametri ir nemainīgi. Risks ir vienīgais parametrs, kuru risku menedžeris var efektīvi mainīt veiksmīgi pārvaldot risku.
Mēs arī varam modelēt daudz sarežģītākas spēles ar veiksmes un atalgojuma matricu un ieraudzīt iespējamo rezultātu diapazonu. Skat. tab. Nr. 1.
|
Veiksme |
Atalgojums |
|
10 % |
zaudējums 2 |
|
20 % |
zaudējums 1 |
|
30 % |
izrāviens |
|
20 % |
laimests 1 |
|
10 % |
laimests 2 |
|
10 % |
laimests 3 |
Tabula Nr. 1. Veiksmes un Atalgojuma matrica, kura uzrāda sešus rezultātus.
Šī matrica varētu modelēt spēli „Noliec – paņem” ar sešpusīgu vilciņu vai pat treidingu.
Tomēr pagaidām atgriezīsimies pie mūsu sākotnējā piemēra ar monētu, jo šeit ir pietiekoši daudz dimensiju, lai noilustrētu daudzās riska pārvaldīšanas koncepcijas. Sarežģītākos piemērus mēs apskatīsim vēlāk.
Optimālā likme
Mūsu piemērā ar monētas mešanu mums ir pastāvīga 50 % veiksme, pastāvīgs atalgojums 2 : 1 un mēs vienmēr liekam uz ģerboni. Lai atrastu risku pārvaldīšanas stratēģiju, mums ir jāatrod likmes pārvaldīšanas veids. Šī problēma ir līdzīga tām, kuras ir jārisina tiem risku menedžeriem, kuru bizness ir tirdzniecība ar akcijām. Labi menedžeri saprot, ka viņi neko nevar padarīt ar veiksmi un atalgojumu. Bet problēma ir tā, ka ir jānosaka cik likt uz akcijām. Mēs savu spēli sākam ar 1,000 $.
Minējumi un sistēmas
Viens no veidiem noteikt likmes lielumu ir minēšana. Mēs varam pamēģināt uzlikt 100 $.
Lai arī likmes, kas balstās uz minējumiem, ir visai populāras un droši vien to proporcionālā daļa reālajā pasaulē ieņem milzīgu daļu, tomēr ir jāpiezīmē, ka šeit pastāv vairākas problēmas: operatoram likmēm ir jāpievērš pastāvīga uzmanība un bez tam tās vairāk ir atkarīgas no kaprīzēm un jūtām, nekā no zinātnes.
Lai uzlabotu stāvokli mēs varētu izdomāt likmju SISTĒMU. Sistēma ir loģiska metode, kura nosaka likmju virkni. Sistēmas priekšrocības attiecībā pret minēšanas metodi ir šādas: (1) mums nav vajadzīgs operators, (2) likme kļūst regulāra, paredzama un secīga un, kas ir ļoti svarīgi (3) mēs varam datorā veikt vēsturisko modelēšanu, lai OPTIMIZĒTU likmju sistēmu.
Neskatoties uz vispārēju piekrišanu, ka sistēmai attiecībā pret minēšanu ir acīmredzamas priekšrocības, ļoti daudziem risku menedžeriem, lai atrastu iespēju labi pārvaldīt risku, patiesībā pašiem ir savas personīgās risku pārvaldīšanas metodes, kas ir pietiekoši precīzas, lai dators tās varētu notestēt.
Mūsu spēle ar monētu tomēr ir diezgan vienkārša un mēs tai varētu izdomāt kaut kādas likmju sistēmas. Bez tam mēs varam šīs sistēmas pārbaudīt un optimizēt to parametrus, lai atrastu labu risku pārvaldīšanas metodi.
Finansētā likme un likme ar finansēto daļu
Mūsu sistēmai ir jānosaka likme. Viens veids, kā noteikt likmi, ir izdarīt pastāvīgu likmi, nu teiksim 10 $, katru reizi neskatoties uz to cik mēs vinnējam vai zaudējam. Šī sistēma saucas FIKSĒTĀ LIKME. Šajā gadījumā, tāpat, kā arī visās citās sistēmās, mūsu AKTĪVS 1,000 $ apmērā var palielināties vai samazināties līdz tādiem apjomiem, kad fiksētā likme 10 $ kļūs proporcionāli pārāk liela vai maza, lai būtu laba.
Lai atbrīvotos no šīs problēmas mēs varam likmi noteikt kā mūsu aktīva FIKSĒTO DAĻU. Fiksētās daļas likme 1 % apmērā no mūsu sākotnējiem aktīviem, no 1,000 $, būtu 10 $. Tomēr šoreiz aktīviem pieaugot vai samazinoties, arī likme visu laiku būs tiem proporcionāla.
Pie fiksētās daļas likmēm pastāv kāds interesants artefakts. Tā kā likme paliek proporcionāla aktīvam, tad teorētiski nav iespējams izputēt, jo oficiālais pilnīga kraha risks ir vienāds ar nulli.
Modelēšana
Lai pārbaudītu mūsu likmju sistēmu, mēs vēsturiskos rezultātus varam MODELĒT. Teiksim, mēs monētu metam desmit reizes un iegūstam piecus ģerboņus un piecus ciparus. Modelēšanas rezultātus mēs varam apskatīt tab. Nr. 2.
|
|
Fiksētā likme 10 $ |
Fiksētā daļa 1 % |
|
Starts |
1000 |
1000 |
|
Ģerbonis |
1020 |
1020 |
|
Cipars |
1010 |
1009.80 |
|
Ģerbonis |
1030 |
1030 |
|
Cipars |
1020 |
1019.70 |
|
Ģerbonis |
1040 |
1040.09 |
|
Cipars |
1030 |
1029.69 |
|
Ģerbonis |
1050 |
1050.28 |
|
Cipars |
1040 |
1039.78 |
|
Ģerbonis |
1060 |
1060.58 |
|
Cipars |
1050 |
1049.97 |
Tabula Nr. 2. Fiksētās likmes un fiksētās daļas sistēmas modelēšana.
Ievērojiet, ka abas sistēmas pirmajā metienā liek 20.00 $ (dubultotu likmi), kur izkrita ģerbonis. Otrajā metienā, kad fiksētās likmes sistēma zaudē 10 $, fiksētās daļas sistēma zaudē 1 % no 1,020.00 $, jeb 10.20 $, un tai paliek 1,009.80 $
Pievērsiet uzmanību, ka abu sistēmu rezultāti ir apmēram vienādi. Tomēr pēc kāda laika fiksētās daļas sistēma eksponentā pieaug un pārsniedz fiksētās likmes sistēmu, kura pieaug lineāri. Tāpat pievērsiet uzmanību, ka rezultāts ir atkarīgs no ģerboņu un ciparu skaita, un nemaz nav atkarīgs no to kārtības. Lasītājs šo rezultātu var pierādīt modelējot savu tabulu.
Piramīdings un Martingeils
Gadījuma rakstura procesos, tādos, kā monētas mešana, ģerboņi un cipari viens aiz otra izkārtojas haotiskā secībā, tā kā to pareizai kārtībai nav nekāda ticamība. Šo parādību tās nejaušību dēļ izmantot neizdosies. Procesos, kas nav nejauši, piemēram, akciju cenu trends, efektīvu pielietojumu var rast PIRAMĪDINGS un citas trendu tirdzniecības metodes.
Piramīdings ir pozīciju palielināšanas metode, kuru pielieto, tad kad tā sāk nest peļņu. Šī tehnika varētu būt lietderīga treiderim, tad, kad tas palielina pozīciju līdz tās optimālajiem izmēriem, taču piramīdings jau optimālās pozīcijas maksimuma punktā novedīs pie katastrofas.
MARTINGEILA sistēma ir dubultošanas metode pie likmes zaudēšanas. Gadījumā, ja arī dubultotā likme tiek zaudēta, mēs dubultošanu turpinām. Šī sistēma ir līdzīga mēģinājumam paķert monētu tuvu braucošas tvaika lokomotīves priekšā. Rezultātā virkne zaudējumu var iznīcināt visu rēķinu.
Optimizācija ar modelēšanas palīdzību
Kā tikko mēs esam izvēlējušies likmju, nu teiksim fiksētās daļas sistēmu, mēs to varam optimizēt atrodot PARAMETRUS, kas mums pavēstīs labāko GAIDĀMO LIELUMU. Monētas mešanas gadījumā mūsu vienīgais parametrs ir fiksētā daļa. Atbildi mēs varam iegūt ar modelēšanas palīdzību. Skat. tab. Nr. 3. un Nr. 4.
Piebilde: piemērs ar monētas mešanu ilustrē dažus riska elementus un to savstarpējo saikni. Tas attiecas uz monētu, kura vinnē 2 : 1 ar iespēju 50 %, ka izkritīs vienāds ģerboņu un ciparu skaits. Šeit netiek apskatīts gadījums, kad ģerboņu un ciparu skaits nav vienāds, vai arī kad tie rada zaudējumu vai laimestu joslu. Šeit netiek piedāvāti specifiskie parametri riskiem tirdzniecībai tirgū.
|
% Likmes |
Starts |
Ērglis |
Cipars |
Ērglis |
Cipars |
Ērglis |
Cipars |
Ērglis |
Cipars |
Ērglis |
Cipars |
|
0 |
1000.00 |
1000.00 |
1000.00 |
1000.00 |
1000.00 |
1000.00 |
1000.00 |
1000.00 |
1000.00 |
1000.00 |
1000.00 |
|
5 |
1000.00 |
1100.00 |
1045.00 |
1149.50 |
1092.03 |
1201.23 |
1141.17 |
1255.28 |
1192.52 |
1311.77 |
1246.18 |
|
10 |
1000.00 |
1200.00 |
1080.00 |
1296.00 |
1166.40 |
1399.68 |
1259.71 |
1511.65 |
1360.49 |
1632.59 |
1469.33 |
|
15 |
1000.00 |
1300.00 |
1105.00 |
1436.50 |
1221.03 |
1587.33 |
1349.23 |
1754.00 |
1490.90 |
1938.17 |
1647.45 |
|
20 |
1000.00 |
1400.00 |
1120.00 |
1568.00 |
1254.40 |
1756.16 |
1404.93 |
1966.90 |
1573.52 |
2202.93 |
1762.34 |
|
25 |
1000.00 |
1500.00 |
1125.00 |
1687.50 |
1265.63 |
1898.44 |
1423.83 |
2135.74 |
1601.81 |
2402.71 |
1802.03 |
|
30 |
1000.00 |
1600.00 |
1120.00 |
1792.00 |
1254.40 |
2007.04 |
1404.93 |
2247.88 |
1573.52 |
2517.63 |
1762.34 |
|
35 |
1000.00 |
1700.00 |
1105.00 |
1878.50 |
1221.03 |
2075.74 |
1349.23 |
2293.70 |
1490.90 |
2534.53 |
1647.45 |
|
40 |
1000.00 |
1800.00 |
1080.00 |
1944.00 |
1166.40 |
2099.52 |
1259.71 |
2267.48 |
1360.49 |
2448.88 |
1469.33 |
|
45 |
1000.00 |
1900.00 |
1045.00 |
1985.50 |
1092.03 |
2074.85 |
1141.17 |
2168.22 |
1192.52 |
2265.79 |
1246.18 |
|
50 |
1000.00 |
2000.00 |
1000.00 |
2000.00 |
1000.00 |
2000.00 |
1000.00 |
2000.00 |
1000.00 |
2000.00 |
1000.00 |
|
55 |
1000.00 |
2100.00 |
945.00 |
1984.50 |
893.03 |
1875.35 |
843.91 |
1772.21 |
797.49 |
1674.74 |
753.63 |
|
60 |
1000.00 |
2200.00 |
880.00 |
1936.00 |
774.40 |
1703.68 |
681.47 |
1499.24 |
599.70 |
1319.33 |
527.73 |
|
65 |
1000.00 |
2300.00 |
805.00 |
1851.50 |
648.03 |
1490.46 |
521.66 |
1199.82 |
419.94 |
965.85 |
338.05 |
|
70 |
1000.00 |
2400.00 |
720.00 |
1728.00 |
518.40 |
1244.16 |
373.25 |
895.80 |
268.74 |
644.97 |
193.49 |
|
75 |
1000.00 |
2500.00 |
625.00 |
1562.50 |
390.63 |
976.56 |
244.14 |
610.35 |
152.59 |
381.47 |
95.37 |
Tabula Nr. 3. Aktīvu modelēšana pielietojot fiksētās daļas sistēmu.
Pie likmes 0 % aktīva izmaiņu nav. Pie likmes 5 % mēs liekam 5 % no 1,000.00 $ vai 50.00 $ un pirmajā metienā tos dubultojam (ģerbonis), tā, ka nu mums ir gaidāmais lielums 1,100 $, kas ir parādīts ar pelēko. Tad nāk mūsu otrā 5 %likme no 1,100.00 $, kas ir 55.00 $. To mēs zaudējam, tāpēc mums paliek 1,045.00 $. Pievērsiet uzmanību, ka laimēšanas parametrs (25 %) pēc vien ērgļa un cipara uzreiz cikla kļūst acīm redzams. Tas mums palīdzēs vienkāršot optimālā parametra meklēšanas problēmu un ekspertīzi samazināt līdz vienam ģerboņu un ciparu parametram.
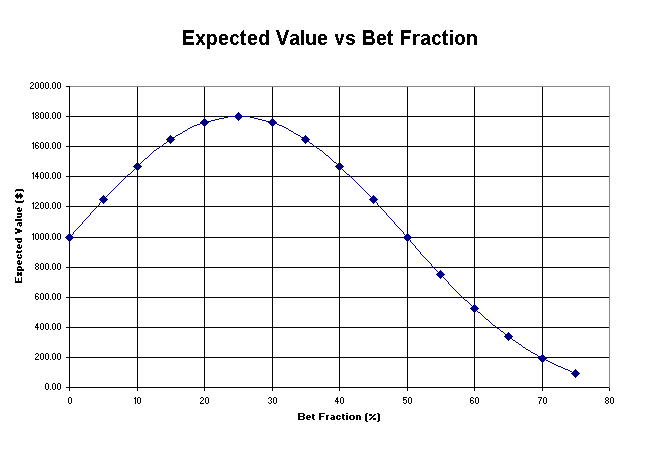
Tabula Nr. 4. Sagaidāmais lielums (beigu aktīvs) pēc desmit metieniem pastāvīgās likmes sistēmai spēlei ar valūtu 2 : 1.
Ievērojiet, ka sistēmas gaidāmais lielums palielinās no 1,000.00 $ līdz maksimālajam lielumam apmēram 1,800.00 $ pie likmes daļas palielināšanas līdz 25 %. Pēc tam līdz ar likmes daļas palielināšanu ienākumi samazinās. Šī līkne atspoguļo divus fundamentālus riska pārvaldīšanas principus: (1) Kautrīgā Treidera noteikums: Ja Jūs neuzliekat daudz, Jūs neuztaisīsiet daudz, un (2) Drosmīgā Treidera noteikums: Ja Jūs liekat par daudz, Jūs esat uz izputēšanas ceļa. Portfeļos, kuri satur lielu daudzumu pozīciju un lielu daudzumu likmju, mēs kopīgo risku uzskatām par portfeļa temperatūru.
Piebilde: pievērsiet uzmanību, ka grafiks ilustrē attiecības Gaidāmo lielumu / Likmes Daļu spēlei ar valūtu 2 : 1. Šo attiecību grafiks pie mainīgām valūtām ir parādīts shēmā Nr. 8.
Optimizācija ar aprēķinu palīdzību
Tā kā mūsu spēle ar monētu ir relatīvi vienkārša, mēs izmantojot aprēķinus varam atrast optimālo likmes daļu. Par cik mēs zinām, ka labākā sistēma ir atpazīstama pēc viena ģerboņu un ciparu cikla, tad mēs problēmas risinājumu varam samazināt tikai līdz vienam pārim ērglis – cipars.
Likme pēc viena pāra ērglis – cipars.
S = (1 + b*P) * (1 - b) * S0
S – likme pēc viena pāra ērglis – cipars
B – likmes daļa
P – izmaksa par uzvaru – 2 : 1
S0 – likme pirms metienu pāra
(1 + b*P) – uzvaras metiena efekts
(1 - b) – zaudējuma metiena efekts
Tad metienu pāra efekts:
R = S / S0
R = (1 + bP) * (1 - b)
R = 1 - b + bP - b2P
R = 1 + b(P-1) - b2P
Pievērsiet uzmanību kā pie b maza apjoma R palielinās par b (P-1), bet pie b liela apjoma R samazinās par b2P. Šīs ir kautrīgā un drosmīgā treideru noteikumu matemātiskie formulējumi.
Mēs R un b varam ievietot grafikā, kurš izskatās līdzīgs tam, kuru mēs ieguvām ar modelēšanas palīdzību, un pārbaudīt maksimālo punktu. Mēs varam pamanīt, ka pie maksimālā sagāzuma tas ir vienāds ar nulli, un tas nozīmē, ka mēs, regulējot sagāzumu tā, lai tas līdzinātos nullei, varam sasniegt maksimumu.
Noliekums = dR/db = (P-1) - 2bP = 0, tad:
b = (P-1)/2P , un, priekš P = 2:1,
b = (2 - 1)/(2 * 2) = 0.25
Tādējādi ir skaidrs, ka optimālā likme tāpat kā iepriekš, arī šobrīd ir vienāda ar 25 % no aktīva.
Optimizācija ar Kelli formulas palīdzību
J. L. Kelly oriģinālais raksts „A New Interpretation of Information Rate”, 1965. g., stāsta par iespējām kā pa telefona līnijām var pārraidīt datus. Viena viņa darba daļa ir veltīta Kelli formulai, kura tiek pielietota, lai optimizētu likmes.
|
Kelli formula |
|
K = W - (1-W)/R |
|
K = Kapitāla daļa nākamajam darījumam
W = vēsturiskā attiecība peļņa/zaudējumi
R = Ieguvuma procents
Piemēram ar monētu, kur ieguvuma procents 2 : 1 ar iespēju 50/50, ka izkritīs ģerbonis vai cipars.
Tad ... K = 0.5 - (1 - 0.5)/2 = 0.5 - 0.25 = 0.25.
Kelli parāda, ka optimālā likme būs 25%. |
Tabula Nr. 5. Kelli formula.
Ievērojiet, ka W un R ir ilgtermiņa vidējie lielumi, tā, ka būs nepieciešams laiks, lai K kaut nedaudz izmainītos.
Dažas grafiskās attiecības starp veiksmi, atalgojumu un likmes optimālo daļu
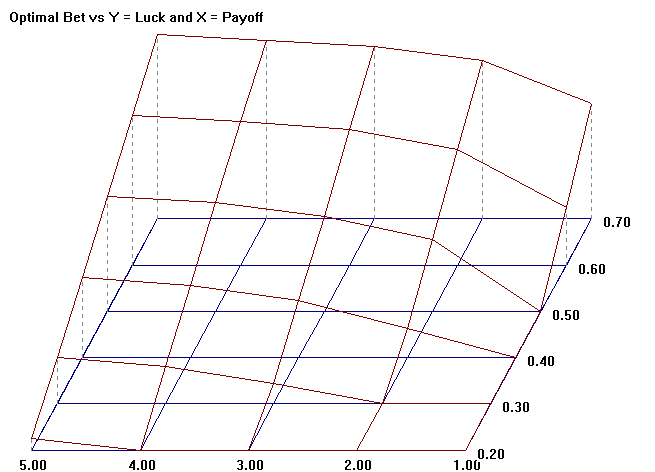
Tabula Nr. 6. Likmes optimālā daļa palielinās lineāri, asimptotiski ar atalgojumu.
Šis grafiks parāda likmes optimālo daļu pie dažāda veiksmes (Y) un atalgojuma (X) lielumiem. Ar atalgojuma pieaugumu pieaug arī likmes optimālā daļa. Pie ļoti lieliem atalgojumiem likmes optimālais izmērs ir vienāds ar veiksmi. Piemēram, pie atalgojuma 5 : 1 un monētas 50/50, optimālā likme pietuvojas 50 %.
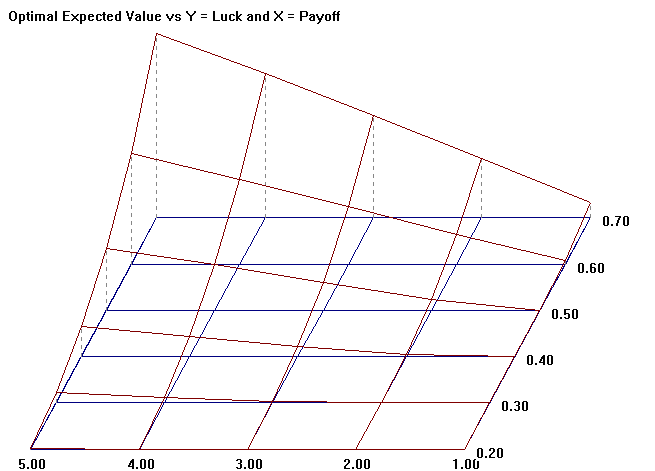
Tabula Nr. 7. Optimālais gaidāmais lielums palielinās ar atalgojumu un veiksmi.
Šis grafiks parāda optimālo gaidāmo lielumu pie dažādiem veiksmes un atalgojuma lielumiem ņemot vērā likmes optimālās daļas. Jo lielāks ir atalgojums (X: no 1:1 līdz 5:1) un jo lielāka veiksme (Y: no 0.20 līdz 0.70), jo lielāks ir gaidāmais lielums. Piemēram, vislielākais gaidāmais lielums – pie 70 %, laimests, izmaksāts 5 : 1. Pats zemākais gaidāmais lielums ir monētai, kura maksā 1 : 1 (savu likmi).
Likmes optimālās daļas atrašana vadoties no likmes lieluma un atalgojuma.
Turpinājums sekos.... |